Persistent data structures thanks to recursive type aliases
7 min read ·
It’s well known that mutability is evil and often troublesome. But, it’s also a fact that mutable data structures are, in some cases, more straightforward to implement and have better performance. Sometimes, you can go with it and be completely fine, but other times immutability is required. Let’s focus on arrays for now. What would you do if you want to append or prepend an item to the list in an immutable way? A shallow copy? A deep copy (god forbid)? These operations are expensive. They have greater asymptotic time complexity — O(n), and what we want is O(1). In this article, I’m going to show a simple data structure that achieves that.
Do I get your attention now? So, let’s start!
Persistent vs immutable data structure 🔎
Firstly, I need to confess. For quite a lot of time, I thought that a persistent structure is just an immutable structure. Pretty lame. Then I got to know that the data structure is persistent when it preserves previous versions of itself when it’s modified. It’s like it never forgets who it was. They are, in fact, effectively immutable, but it doesn’t work the other way around. Immutable data structures don’t have to be necessarily persistent.
You can read more about it here.
Meet Cons List
And here it is. Star of the show 👏
Firstly, let’s focus on what cons means. So… it’s a function. What’s more, it’s the fundamental function in many programming languages. Especially in Lisp dialects. It takes two objects or pointers to the objects x and y and constructs object in the memory holding x and y. When it comes to cons lists, it takes a value, and the cons list and constructs brand new object out of it, which is also cons list. You may have seen this before:
-
1::[2]: ML, Scala, F# and Elm
-
1:[2]: Haskell
-
(cons 1 2): Lisp and it’s dialects
The above are the constructors for the list data structure. cons list is also called a linked list, which I guess, is a more recognizable name.
We can visualize cons list in the following way:
┌────────────┐ ┌────────────┐ ┌────────────┐
│ 1 | tail │ ┌─│ 2 | tail │ ┌─│ 3 | null │
└────────│───┘ │ └────────│───┘ │ └────────────┘
└───────┘ └───────┘
a linked list of (1, 2, 3)
How is it persistent?
There were a few words about persistent data structures, so you may wonder if cons list is persistent. Yes, it is! Let’s see how.
Let’s say we have a cons list — xs, and we want to cons an element to it. It results in a brand new list ys, and what you can notice is that items from xs are now shared between xs and ys. Thus the list xs hasn’t been modified, and it’s a part of the new list ys.
xs ys
┌──│──┐ ┌──│──┐
│ 3 │ │ 4 │
└──│──┘ └──│──┘
┌──│──┐ xs │
│ 2 │ cons 4 xs → └─┌┘
└──│──┘ ┌──│──┐
┌──│──┐ │ 3 │
│ 1 │ └──│──┘
└─────┘ ┌──│──┐
│ 2 │
└──│──┘
┌──│──┐
│ 1 │
└─────┘
How it looks in TypeScript 3.7
I can write the type of cons list in the following way and it perfectly works thanks to recursive type aliases introduced in TypeScript 3.7.
ts
ts
Before 3.7, I would get the following error:
Type alias ‘ConsList’ circularly references itself. ts(2456)
Long story short, type aliases needed to be eagerly built, so you couldn’t have on the right side the same thing as on the left side because the compiler would try to substitute the former with the later and then the later with the former and so on… You can read more about it on TypeScript 3.7 announcement.
Functions operating on ConsList
Okay, so we already have some overview of what cons list is. Now it’s time to see what we can do with it and how to make it useful. cons list may come as an immutable replacement for Array. That means we can expect it to have some of its functionalities. Let’s add some!
- Prepend element to list
ts
ts
- Extract head and tail from the list
ts
ts
- Map over it.
Note: cons list with map is no longer persistent. It’s just immutable. To make it persistent, we would need to memorize previous versions. I’ll skip it for now.
ts
ts
- Reduce it
ts
ts
- Construct a new cons list from Array and vice versa
ts
ts
- Reverse it
ts
ts
- Concat two cons lists
ts
ts
So far, so good. I’ll stop now. It’s pretty powerful already 💪
Real-life use cases 🛠
As you might have noticed, the cons list gives us rapid access to the first element of the list. That means we can prepend to the list and take the first element from it extremely fast. As a matter of fact, a stack (or last-in-first-out queue) is the data structure that is based on these two operations. Push to the stack is just doing cons on the cons list, and pop is extracting the head. In common stack nomenclature it would go like that:
const push = cons;
const pop = tail;
const peek = head;
Great! We have stack done effortlessly. Without any modifications and without any new code. That one was easy, now it is time for something more complex. First-in-first-out queue. The structure when we are taking elements from the front and pushing to the end. So, we need rapid access to both the first and last element of the list. It’s pretty straightforward with mutations and pointers. We would only need to maintain two pointers for the first and the last item. But we don’t have mutations. We have our cons list instead!
There was this smart guy named Chris Okasaki, who came up with a clever way how to implement an effective, immutable FIFO quque, using a pair of two cons lists (front, back). They are representing, respectively, the front and the back of the queue. But the back is reversed, so the head of this list is the last element of the queue.
ts
ts
Key points of this structure:
- When we want to push an item to the queue, we need to prepend it to the back
- When we want to pop an item, we need to extract the head from front
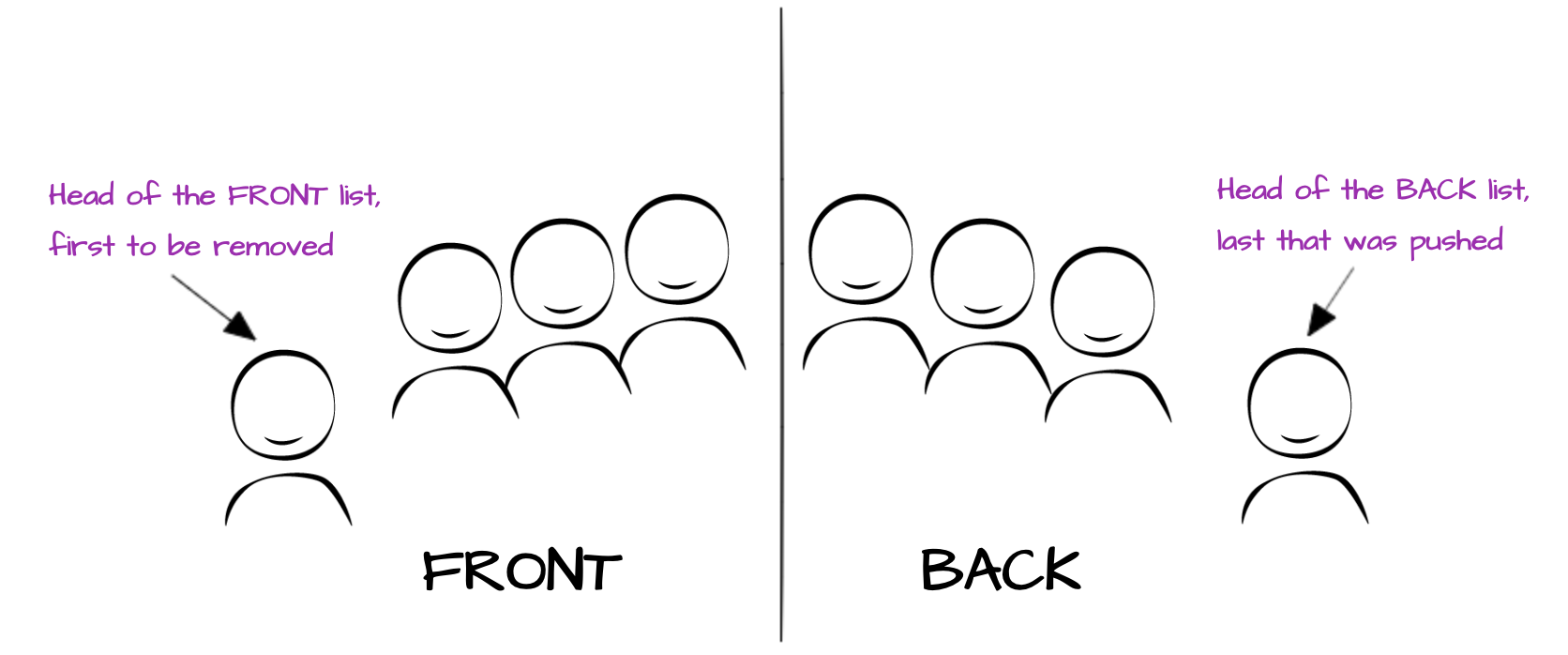
When we keep pushing elements to the queue, they all will drift into the back list. Let’s say we pushed one after another numbers from 1 to 5. That means our structure would look somehow like this:
ts
ts
The front list is empty. So how can we take an element out of it? That’s the best part. We do a rotation. That means we take the back list, reverse it, attach it as the new front and make back empty.
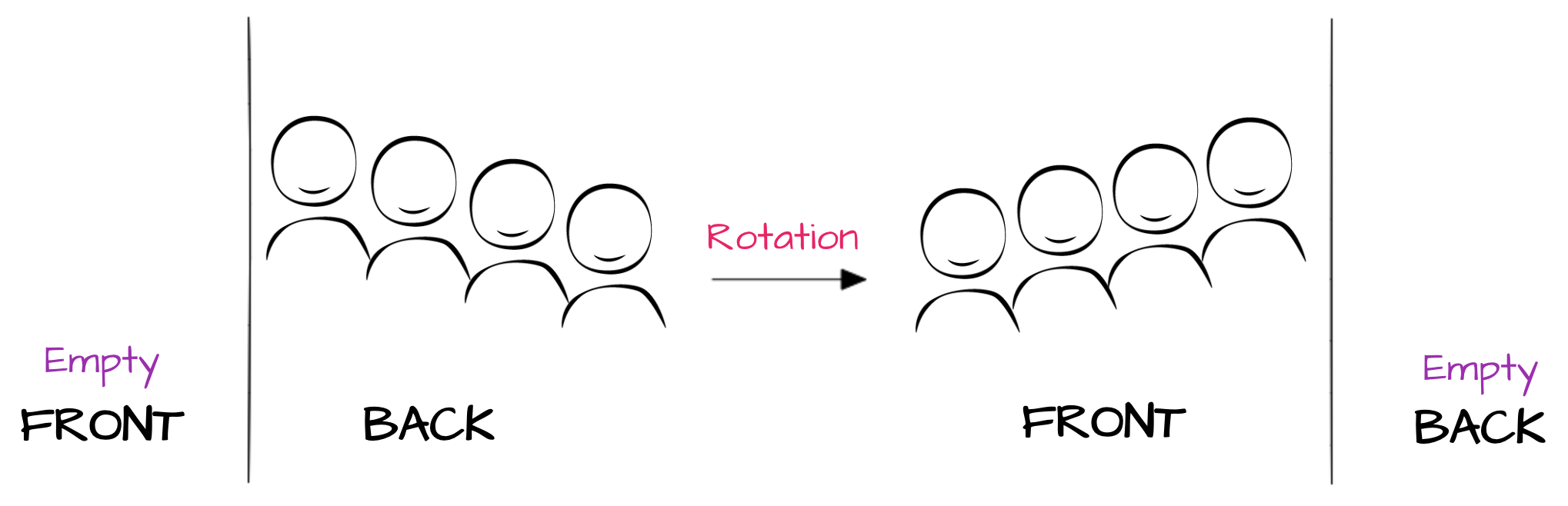
Here’s the whole implementation:
ts
ts
When not to use cons list
- It’s not a replacement to Array.
- It’s not a random access list (thus I didn’t even implement it), so if you want fast random access then better use Array.
Benchmarks ⌛️
You may wonder if using cons lists pays off somehow. In fact, it does! I did some benchmarks comparing operations on Array and on cons list and the results are thrilling! Here’s the gist with benchmarks.
Mutable operations vs cons
| Opeation | ops/s |
|---|---|
| array.unshift(50) | 99953.939 |
| array.push(50) | 70675.276 |
| cons(50, list) | 5822999.798 |
Immutable operation vs cons
| Operation | ops/s |
|---|---|
| [50, …array] | 12680.588 |
| cons(50, list) | 5485947.933 |
Array.prototype.map vs map
| Operation | ops/s |
|---|---|
| array.map(x => x * 2) | 4389.837 |
| map(list, x => x * 2) | 662.805 |
I hope the above benchmarks speak for themselves. It’s kind of funny because I expected a cons list map to be a little bit slower, but it surprisingly fast. If you know why let me know 😛